ハッシュ計算処理

2009年05月26日（火）

前ページのパディング処理によって入力データは64Byteできれいに切り分けられるようになりました。続くハッシュ計算処理がSHA-256の中枢部になります。ハッシュ関数によってはサインやコサインなどの三角関数を使うものがありますが、SHAでは三角関数を使わず、値の加算・ビットシフト・ビット回転・XOR演算などによって計算します。三角関数が苦手なWIZ.にとってはありがたい話です♪

ハッシュ計算処理の手順

さて、ハッシュ計算処理に必要な情報は、入力データを64Byteで切り分けた「メッセージブロック」と「初期ハッシュ値（２回目以降は算出されたハッシュ値）」です。また、ハッシュ計算処理の中では、ハッシュ値を256bitの値としてではなく、8つの32bit値に分けて処理します。この8つハッシュの素に対してどのような処理を行っていくのかを見てみましょう。

ローテーション処理

「ローテーション処理」は私が名づけたものです。 FIPSにこの処理を明確に示す名称がなかったので勝手に名づけました。ここでは何をするかというと、８つに分けたハッシュ値を順番に入れ替えていきます。

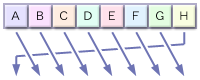
メッセージ処理の開始時点では、8つの32bit値が右図のような並びになっているとします。これを一度ローテーション処理にかけると…

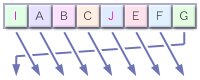
このようにひとつずつ移動します。よく見ると、ＡＢＣとＥＦＧの6つはそのまま右にスライドしただけですが、ＤがＪに、ＨがＩに変化しています。さらに次の回転をすると…

またしても、１番目と５番目が変化しました。これがローテーション処理で、１回のハッシュ計算処理につきローテーション処理が64回行われます。わずかに変化したデータでも全く異なるメッセージダイジェストが作られるからくりがここにあるわけです。

下図の出力結果は、実際に「abc」を入力データとしてローテーション処理を実行した結果です。ローテーション処理を行うごとに値が右へスライドし、5番目に遷移する際に値が変化しているのがわかります。

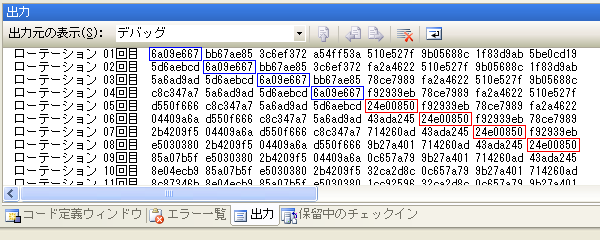
では１番目と５番目はどのような規則で変化しているのでしょうか。この変化を与えている材料のひとつが「メッセージブロック」です。

メッセージブロックの拡張処理

メッセージブロックは64Byte。ローテーション処理は64回。この数字の一致から、ローテーション処理１回につき、メッセージブロックのデータが1Byte使われる、と考えるかもしれませんね。えぇ、私のことです。ですが、実際は違います。ローテーション処理に入る前に、メッセージブロックは64Byteから4倍の256Byteに拡張されます。

まず、メッセージブロックを4Byteずつ区切り、16個の32bit値(W)へ変換します。

[        Message Block (64Byte)       ]
[ W(1) ][ W(2) ][ W(3) ]......[ W(16) ]

次に、W(17)～W(64)個目までをここまでの値を元に算出します。これは、次の計算で求められます。

W(n) = W(n-2) + W(n-7) + W(n-15) + W(n-16)

ただし、nは17以上。 32bit値を超えた分（オーバーフロー）は破棄します。例えばW(17), W(64)の場合は次のようになります。

W(17) = W(15) + W(10) + W(2) + W(1)
W(64) = W(62) + W(57) + W(49) + W(48)

このようにして、64個の32bit値（つまり4Byte×64で256Byte）が生成されます。これらが、ローテーション処理１回につき１個ずつ使用されるのです。さらにローテーション処理にはもうひとつの材料が必要です。それが「定数k」と呼ばれる定数郡です。